在一般的数据结构的书中,树的那章后面,著者一般都会介绍一下哈夫曼(HUFFMAN)
树和哈夫曼编码。哈夫曼编码是哈夫曼树的一个应用。哈夫曼编码应用广泛,如
JPEG中就应用了哈夫曼编码。
什么是哈夫曼树
首先介绍什么是哈夫曼树。哈夫曼树又称最优二叉树,
是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的 路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。
编码步骤
- 对给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵二叉树的初始集合
F={T1,T2,T3,...,Ti,...,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。(为方便在计算机上实现算法,一般还要求以Ti的权值Wi的升序排列。) - 在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
- 从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
- 重复二和三两步,直到集合F中只有一棵二叉树为止。
简单的理解就是,假如我有A,B,C,D,E五个字符,出现的频率(即权值)分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树,即取1,2构成新树,其结点为1+2=3,如图: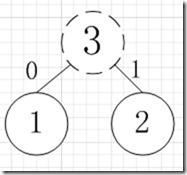
虚线为新生成的结点,第二步再把新生成的权值为3的结点放到剩下的集合中,所以集合变成{5,4,3,3},再根据第二步,取最小的两个权值构成新树,如图: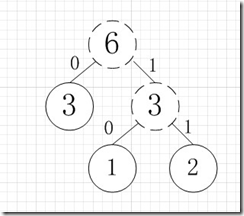
再依次建立哈夫曼树,如下图: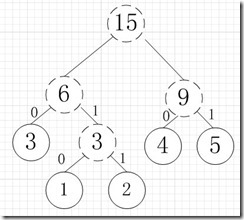
其中各个权值替换对应的字符即为下图: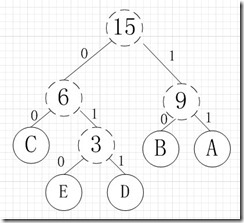
所以各字符对应的编码为:A->11,B->10,C->00,D->011,E->010
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩,加密解密等场合。
个人理解
- 构造一个哈夫曼树,首先要把那些带权值的叶子节点从小到大排序
- 挑出最小的两个,构成一个二叉树,小的在左边
- 然后把这时候,这两个节点相加的出来的父节点的值,放入到刚才的那个带权值的数组中去,然后重复这个步骤,挑出一个最小的然后继续画?应该就是这样
- 哈弗曼编码就是左边是0,右边是1,然后边数边写,从根节点开始往下走